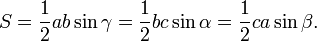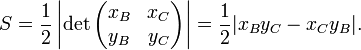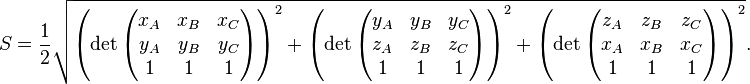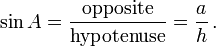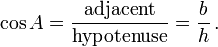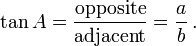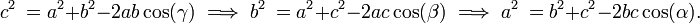Introduction to Trigonometry

Definitions and basics

Trigonometric circle and angles

Take an x-axis and an y-axis (orthonormal) and let O be the origin.
A circle centered in O and with radius = 1, is called a trigonometric circle or unit circle.
Turning counterclockwise is the positive orientation in trigonometry.
Angles are measured starting from the x-axis.
Two units to measure an angle are degrees and radians
An orthogonal angle = 90 degrees = pi/2 radians
In this theory we use mainly radians.
With each real number t corresponds just one angle, and just one point P on the unit circle, when we start measuring on the x-axis. We call that point the image point of t.

Examples:

• with pi/6 corresponds the angle t and point P on the circle.
• with -pi/2 corresponds the angle u and point Q on the circle.

Trigonometric numbers of a real number t

With t radians corresponds exactly one point p on the unit circle.

• The x-coordinate of P is called the cosine of t. We write cos(t).
• The y-coordinate of P is called the sine of t. We write sin(t).
• The number sin(t)/cos(t) is called the tangent of t. We write tan(t).
• The number cos(t)/sin(t) is called the cotangent of t. We write cot(t).
• The number 1/cos(t) is called the secant of t. We write sec(t)
• The number 1/sin(t) is called the cosecant of t. We write csc(t)

The line with equation sin(t).x - cos(t).y = 0
contains the origin and point P(cos(t),sin(t)). So this line is OP.
On this line we take the intersection point S(1,?) with the line x = 1.
It is easy to see that ? = tan(t).
So tan(t) is the y-coordinate of the point S.

Analogous cotan(t) is the x-coordinate of the intersection point S' of the line OP with the line y = 1.

Basic formulas

With t radians corresponds exactly one point p(cos(t),sin(t)) on the unit circle. The square of the distance [OP] = 1. Calculating this distance with the coordinates of P we have for each t :

cos2(t) + sin2(t) = 1

                   sin2(t)
1 + tan2(t) = 1 + ----------
                   cos2(t)

            cos2(t)+sin2(t)
          = -----------------
                cos2(t)


                 1
          = ----------- = sec2(t)
              cos2(t)

Analogous :

1 + cotan2(t) = 1/ sin2(t) = csc2(t)

cos2(t) + sin2(t) = 1 1 + tan2(t) = sec2(t) 1 + cotan2(t) = csc2(t)

Related values

supplementary values

t and t' are supplementary values <=> t+t' = pi.

With the help of a unit circle we see that the corresponding image points are symmetric with respect to the Y-axis. Hence, we have :

If t and t' are supplementary values then sin(t) = sin(t') cos(t) = -cos(t') tan(t) = -tan(t') cot(t) = -cot(t')

complementary values

t and t' are complementary values <=> t+t' = pi/2.

The corresponding image points on a unit circle are symmetric with respect to the line y = x . Hence, we have :

If t and t' are complementary values then sin(t) = cos(t') cos(t) = sin(t') tan(t) = cot(t') cot(t) = tan(t')

Opposite values

t and t' are opposite values <=> t+t' = 0.

Now, the corresponding image points are symmetric with respect to the X-axis. Hence, we have :

If t and t' are opposite values then sin(t) = -sin(t') cos(t) = cos(t') tan(t) = -tan(t') cot(t) = -cot(t')

Anti supplementary values

t and t' are anti supplementary values <=> t-t' = pi.

The corresponding image points are symmetric with respect to the origin O . Hence, we have :

If t and t' are anti-supplementary values then sin(t) = -sin(t') cos(t) = -cos(t') tan(t) = tan(t') cot(t) = cot(t')

The right-angled triangle

Say the angle A is the right angle of the triangle ABC. The distances |AB|, |BC| and |CA| are usualy denoted by c, a and b. Take point B in a suitable way as center of a trigonometric circle (see figure).

Now sin(B),cos(B) and 1 are directly propertional with b, c and a.

       sin(B)   cos(B)    1
       ------ = ------ = ---
         b        c       a

=>      sin(B) = b/a   cos(B) = c/a  tan(B) = b/c

and since the angles B and C are complementary angles

       cos(C) = b/a   sin(C) = c/a   tan(C) = c/b

In each right-angled triangle ABC, with A as right angle, we have sin(B) = b/a cos(B) = c/a tan(B) = b/c cos(C) = b/a sin(C) = c/a tan(C) = c/b

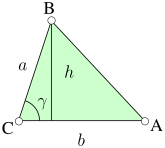
Area of a triangle

The area of the triangle is a.h/2 .
But in triangle BAH, we have sin(B) = h/c .
Hence the area of the triangle is a.c.sin(B)/2.
Similarly we have that the area of the triangle
= b.c.sin(A)/2 = a.b.sin(C)/2

The area of a triangle ABC = a.c.sin(B)/2 = b.c.sin(A)/2 = a.b.sin(C)/2

Sine rule

In a triangle ABC we have seen that the area =

       a.c.sin(B)/2 =  b.c.sin(A)/2 = a.b.sin(C)/2
=>
       a.c.sin(B) =  b.c.sin(A) = a.b.sin(C)

dividing through by  a.b.c, we get

In any triangle ABC we have a b c ------ = ------ = ------ sin(A) sin(B) sin(C)

This formule is called the sine rule in a triangle ABC. Say R is the radius of the circle with center O through the points A,B and C. Let B' be the second intersection point of BO and the circle. The angle B' in triangle BB'C is equal to A. In the right-angled triangle BB'C we see that a = 2R sin(B') = 2R sin(A). Thus, The fractions in the sinus rule are all equal to 2R.

Homogeneous expression in a, b and c

If an expression between the sides of a triangle is homogeneous in a, b and c, we have an equivalent expression by replacing a,b and c with sin(A), sin(B), sin(C).

Example:
In a triangle

       b.sin(A-C) = 3.c.cos(A+C)
<=>
       sin(B).sin(A-C) = 3.sin(C).cos(A+C)

Cosine rule

In any triangle ABC we have a2 = b2 + c2 - 2 b c cos(A) b2 = c2 + a2 - 2 c a cos(B) c2 = a2 + b2 - 2 a b cos(C)

Proof:
This rule is deduced using the dot product of vectors.
See Proof cosine rule

Trigonometric functions

The sine function

The function defined by :

sin : R -> R : x -> sin(x)

is called, the sine function.
The images are bounded in [-1,1] and the period is 2.pi .
We say that the range of the function is [-1,1].

The cosine function

The function defined by :

cos : R -> R : x -> cos(x)

is called, the cosine function.
The images are bounded in [-1,1] and the period is 2.pi .
The range of the function is [-1,1].

The tangent function

The function defined by :

tan : R -> R : x -> tan(x)

is called, the tangent function.
Now, the period is pi and the images are not defined in x = (pi/2) + k.pi
The range or image is R.

The cotangent function

The function defined by :

cot : R -> R : x -> cot(x)

is called, the cotangent function.
The period is pi and that the images are not defined in x = k.pi
The range or image is R.

Inverse Trigonometric Functions

The arcsin function

We restrict the domain of the sine function to [-pi/2 , pi/2].
Now this restriction is invertible because each image value in [-1,1] has just one origin in [-pi/2 , pi/2].
The inverse function of that restricted sine function is called the arcsine function.
We write arcsin(x) or asin(x).
The graph y = arcsin(x) is the mirror image of the restricted sine graph with respect to the line y = x.
The domain is [-1,1] and the range is [-pi/2 , pi/2].

The arccos function

We restrict the domain of the cosine function to [0 , pi].
Now this restriction is invertible because each image value in [-1,1] has just one origin in [0 , pi].
The inverse function of that restricted cosine function is called the arccosine function.
We write arccos(x) or acos(x) .
The graph y = arccos(x) is the mirror image of the restricted cosine graph with respect to the line y = x.
The domain is [-1,1] and the range is [0 , pi].

The arctan function

We restrict the domain of the tangent function to [-pi/2 , pi/2].
Now this restriction is invertible because each image value in has just one origin in [-pi/2 , pi/2].
The inverse function of that restricted tangent function is called the arctangent function. We write arctan(x) or atan(x) . The graph y = arctan(x) is the mirror image of the restricted tangent graph with respect to the line y = x.
The domain is R and the range is [-pi/2 , pi/2].

The arccot function

We restrict the domain of the cotangent function to [0 , pi].
Now this restriction is invertible because each image value in has just one origin in [0 , pi].
The inverse function of that restricted cotangent function is called the arccotangent function.
We write arccot(x) or acot(x) .
The graph y = arccot(x) is the mirror image of the restricted cotangent graph with respect to the line y = x.
The domain is R and the range is [0 , pi].

Sum formulas

cos(u - v)

We prove this formula using the concept of dot product of two vectors. (See theory about vectors) With u corresponds one point p(cos(u),sin(u)) on the unit circle
With v corresponds one point q(cos(v),sin(v)) on the unit circle
The angle, corresponding with the arc qp of the circle, has a value u - v .
Now : p.q = 1.1.cos(u-v) .
But using the coordinates we also have p.q = cos(u).cos(v)+sin(u).sin(v).
Hence,

cos(u-v) = cos(u).cos(v)+sin(u).sin(v)

cos(u + v)

cos(u + v) = cos(u - (-v)) = cos(u).cos(-v)+sin(u).sin(-v)

cos(u + v) = cos(u).cos(v)-sin(u).sin(v)

sin(u - v)

sin(u - v) = cos(pi/2-(u-v)) = cos( (pi/2-u) +v )
= cos(pi/2 - u).cos(v)-sin(pi/2 - u).sin(v)

sin(u - v) = sin(u).cos(v)-cos(u).sin(v)

sin(u + v)

sin(u + v) = cos(pi/2-(u+v)) = cos( (pi/2-u) -v )
= cos(pi/2 - u).cos(v)+sin(pi/2 - u).sin(v)

sin(u + v) = sin(u).cos(v)+cos(u).sin(v)

tan(u + v)

           sin(u + v)    sin(u).cos(v)+cos(u).sin(v)
tan(u+v) = ------------ = ---------------------------
           cos(u + v)    cos(u).cos(v)-sin(u).sin(v)

Dividing the dominator and denominator by cos(u).cos(v) we have

tan(u) + tan(v) tan(u+v) = ----------------- 1 - tan(u).tan(v)

tan(u - v)

In the same way, we have

tan(u) - tan(v) tan(u-v) = ----------------- 1 + tan(u).tan(v)

sin(2u)

sin(2u) = sin(u + u) = sin(u).cos(u)+cos(u).sin(u) = 2sin(u).cos(u)

sin(2u) = 2sin(u).cos(u)

cos(2u)

cos(2u) = cos(u+u) = cos(u).cos(u)-sin(u).sin(u) = cos² (u) - sin² (u)

cos(2u) = cos2 (u) - sin2 (u)

tan(2u)

          tan(u) + tan(u)            2 tan(u)
tan(2u) =   ------------------  =  ---------------
          1 - tan(u).tan(u)        1- tan(u)tan(u)

2 tan(u) tan(2u) = ----------- 1- tan2(u)

Carnot formulas

1 + cos(2u) =  1+cos2 (u)-sin2 (u) =  2 cos2 (u)

1 - cos(2u) =  1-cos2 (u)+sin2 (u) =  2 sin2 (u)

1 + cos(2u) = 2 cos2 (u) 1 - cos(2u) = 2 sin2 (u)

t-formulas

From the Carnot formulas we have

cos(2u)  =  2 cos2(u) -1


      2
=  ------------ - 1
  1 + tan2 (u)


  1 -  tan2(u)
=  -------------
  1 + tan2 (u)


We know:
           2 tan(u)
tan(2u)=  -------------
         1 - tan2 (u)

Hence,

            2 tan(u)
sin(2u) =  -----------
          1 + tan2 (u)

Let t = tan(u) , then 1 - t2 cos(2u) = --------- ; 1 + t2 2t sin(2u) = -------- ; 1 + t2 2t tan(2u) = ------- ; 1 - t2

These 3 formulas are called the t-formulas.

Special values

pi/3

Let v be the image point corresponding with the angle pi/3 on the unit circle and let e the intersection point of that circle with the X-axis.
The triangle 'ove' is regular. Hence cos(pi/3) = 1/2.

sin2 (pi/3) = sqrt( 1 - cos2 (pi/3)) = sqrt(3)/2

So, sin(pi/3) = sqrt(3)/2 and cos(pi/3) = 1/2.

pi/4

Let v be the image point corresponding with the angle pi/4 on the unit circle. From this, it is obvious that cos(pi/4) = sin(pi/4) and tan(pi/4) = 1.

cos2(pi/4)+sin2(pi/4) = 1  => 2cos2(pi/4) = 1 =>  cos (pi/4) = sqrt(1/2)

So, cos (pi/4) =  sin(pi/4) = sqrt(1/2)

pi/6

From properties for complementary angles we have: cos (pi/6) = sqrt(3)/2 and sin(pi/6) = 1/2.

Trigonometric equations

Base equations

cos(u) = cos(v)

With the help of a unit circle it is easy to see that
cos(u) = cos(v) <=> (u = v + k.2pi) or (u = -v + k.2pi)

sin(u) = sin(v)

With the help of a unit circle it is easy to see that
sin(u) = sin(v) <=> (u = v + 2.k.pi) or (u = pi - v + 2.k.pi)

tan(u) = tan(v)

With the help of a unit circle it is easy to see that
tan(u) = tan(v) <=> (u = v + k.pi)

cot(u) = cot(v)

With the help of a unit circle it is easy to see that
cot(u) = cot(v) <=> (u = v + k.pi)

Reducing to base equations

Example 1

cos(2x) = cos(pi-3x)
<=>
2x = (pi-3x) + 2.k.pi  or 2x = -(pi-3x) + 2.k'.pi
<=>
5x = pi + 2.k.pi  or    -x = -pi + 2.k'.pi
<=>
x = pi/5 + 2.k.pi/5  or   x = pi - 2.k'.pi

Example 2

tan(x-pi/2) = tan(2x)
<=>
(x-pi/2) = 2x + k.pi
<=>
-x = pi/2 + k.pi
<=>
x = -pi/2 - k.pi

Example 3

cos(x) = -1/3
<=>
cos(x) = cos(1.91)
<=>
x = 1.91 +2.k.pi  or x = -1.91 - 2.k.pi

Example 4

sin(2x) = cos(x-pi/3)
<=>
cos(pi/2 - 2x) = cos(x-pi/3)
<=>
pi/2 - 2x = x - pi/3 + 2.k.pi   or  pi/2 - 2x = - x + pi/3 + 2.k'.pi
<=>
-3x = - pi/2 - pi/3 + 2.k.pi   or  -x =  -pi/2 + pi/3 + 2.k'.pi
<=>
x = pi/6 + pi/9 + 2.k.pi/3   or  x = pi/2 -  pi/3 - 2.k'.pi
<=>
x = 5pi/18  + 2.k.pi/3   or  x = pi/6 - 2.k'.pi

Using an additional unknown

Example 1

2sin2 (2x)+sin(2x)-1=0

<=>             (let t = sin(2x) )

2t2 + t - 1 = 0

<=>

t = 0.5  or t = -1

<=>

sin(2x) = 0.5  or sin(2x) = -1

<=>

sin(2x) = sin(pi/6)   or  sin(2x) = sin(-pi/2)

<=>

2x = pi/6 +2.k.pi or 2x = pi - pi/6 +2.k.pi or
       2x = -pi/2 +2.k.pi or 2x = pi + pi/2  +2.k.pi
<=>

x = pi/12 + k.pi  or x = 5pi/12 + k.pi or
       x = -pi/4 + k.pi  or x = 3pi/4 + k.pi

Sometimes it is convenient to view these solutions on the unit circle. Example 2

    cos 10x + 7 = 8 cos 5x
<=>
    cos 10x - 8 cos 5x + 7 =0
<=>
    1 +  cos 10x - 8 cos 5x + 6 =0
<=>
    2 cos2 5x - 8 cos 5x + 6 =0
<=>

    cos2  5x - 4 cos 5x + 3 = 0

say  t = cos 5x

   t2 - 4t + 3 = 0
<=>
    t = 3  or  t = 1
<=>
    cos 5x  = 1
<=>
    cos 5x = cos 0
<=>
    5x = 2kpi
<=>
    x =  2kpi / 5

Examples
In the same way, the following equations can be solved using an additional unknown.

tan2 (3x)+tan(3x)=0

sin2 (x)(sin(x)+1)-0.25(sin(x)+1) = 0

cos(2x)+sin2 (x) = 0.5


tan(2x)-cot(2x) = 1

Using factorization

Example 1

3.sin(2x)-2.sin(x) = 0

<=>

6sin(x)cos(x)-2.sin(x) = 0

<=>

2.sin(x).(3cos()-1) = 0

<=>

sin(x) = 0  or cos(x) = 1/3

<=>

x = k.pi  or x = 1.23 + 2.k.pi or x = -1.23 + 2.k'.pi

Examples
In the same way, the following equations can be solved using factorization.

tan(x)tan(4x)+tan2 (x) = 0

sin(5x)+sin(3x) = cos(2x)-cos(6x)

The equation a.sin(u)+b.cos(u) = c

First we'll show that a.sin(u)+b.cos(u) can be transformed in the form
A.sin(u-u_o) or in the form A.cos(u-u_o) .

  a.sin(u) + b.cos(u)

=  a( sin(u) + (b/a) cos(u) )

     Take uo such that tan(uo) = - b/a

=  a( sin(u) -  tan(uo)  cos(u) )

=  (a/cos(uo)) . ( sin(u).cos(uo) - sin(uo).cos(u) )

     Let A =  (a/cos(uo))

=  A . sin(u - uo)

=  A . cos(pi/2 - u + uo)

=  A . cos(u - uo')

With this method we can solve the equation
a.sin(u)+b.cos(u) = c

Example

3.sin(2x)+4.cos(2x) = 2

<=>

sin(2x) + 4/3 .cos(2x) =  2/3
               Let tan(t) =  4/3
<=>

sin(2x) + tan(t) .cos(2x) =  2/3

<=>

sin(2x)cos(t)+cos(2x)sin(t) = 2/3.cos(t)

<=>

sin(2x+t) = 2/3.cos(t)

               since 2/3.cos(t) =  0.4
<=>

sin(2x+0.927) = sin(0.39)

<=>

2x + 0.927  = 0.39 +2.k.pi  or 2x + 0.927  =  pi - 0.39 +2.k'.pi

<=>

....

Homogeneous equations

We have in view the equations, witch are homogeneous in sin(u) and cos(u).
Procedure

1. If possible, use factorization and solve the simple parts
2. Divide the remaining equation by a suitable power of cos(u), such that tan(u) appears everywhere.
3. Let t = tan(u) and solve the algebraic equation.
4. Return to tan(u)

Example

2.cos3 (x)+2.sin2 (x)cos(x) = 5.sin(x)cos2 (x)

<=>

cos(x).(2.cos2 (x)+2.sin2 (x) - 5.sin(x)cos(x))  =  0

<=>

The first part  cos(x) = 0 gives us x = pi/2 + k.pi


In the second part, we divide both sides by cos2 (x). Then we have

2.tan2 (x) - 5.tan(x) +2 = 0

               Let t = tan(x)
<=>

2.t2  - 5 t + 2 = 0

<=>

t = 0.5  or t = 2

<=>

tan(x) = 0.5 or tan(x) = 2

<=>

x = 0.464 +k.pi or x = 1.107 +k.pi

Calculations with inverse trigonometric functions

Example

                                 ________
                                |      2
                                | 1 - p
Show that :   cot(arcsin(p))  =  | ------
                               \|   p

       let b = arcsin(p) , then sin(b) = p with b in [-pi/2 , pi/2].


       So, cos(b) = 1 - p 2              and
                                     ________
                                    |      2
                                    | 1 - p
       cot(arcsin(p)) = cot(p) =    | ------
                                   \|   p

Example

Solve : arcsin(2x) = pi/4 + arxsin(x)           (1)
Solution:
       Let arcsin(2x) = a and arcsin(x) = b .
       Then a and b are in [-pi/2 , pi/2].
We have to solve :
       a = pi/4 + b                    (2)

=>      sin(a) = sin(pi/4 + b)

                cos(b) + sin(b)
=>      sin(a) = ---------------
                      ___
                     V 2

                                                     ________
      Since:  sin(a) = 2x, sin(b) = x and cos(b) =  V 1 - x2

                 ________
                V 1 - x2   + x
=>       2x =   ------------------
                     ___
                    V 2

            ___             __________
=>      ( 2.V 2    - 1 )x = V 1 - x2

            ___
=>      (2. V 2  - 1)2 .x2   =  1-x2

=>      x = +0.4798   or x = -0.4798            (3)

Each solution of (1) is in (3), but the reverse is not true.
It is simple to calculate that -0.4798 is not a solution of (1),
and +0.4798 is.
So the only solution is 0.4798 .

Coordinate Geometry

Introduction to Coordinate Geometry

A system of geometry where the position of points on the plane is described using a pair of numbers.

Recall that a plane is a flat surface that goes on forever in both directions. If we were to place a point on the plane, coordinate geometry gives us a way to describe exactly where it is by using two numbers.

What are coordinates?

To introduce the idea, consider the grid on the right. The columns of the grid are lettered A,B,C etc. The rows are numbered 1,2,3 etc from the top. We can see that the X is in box D3; that is, column D, row 3.

D and 3 are called the coordinates of the box. It has two parts: the row and the column. There are many boxes in each row and many boxes in each column. But by having both we can find one single box, where the row and column intersect.

The Coordinate Plane

In coordinate geometry, points are placed on the "coordinate plane" as shown below. It has two scales - one running across the plane called the "x axis" and another a right angles to it called the y-axis. (These can be thought of as similar to the column and row in the paragraph above.) The point where the axes cross is called the origin and is where both x and y are zero.

On the x-axis, values to the right are positive and those to the left are negative.
On the y-axis, values above the origin are positive and those below are negative.

A point's location on the plane is given by two numbers, one that tells where it is on the x-axis and another which tells where it is on the y-axis. Together, they define a single, unique position on the plane. So in the diagram above, the point A has an x value of 20 and a y value of 15. These are the coordinates of the point A, sometimes referred to as its "rectangular coordinates".

For a more in-depth explanation of the coordinate plane see The Coordinate Plane.
For more on the coordinates of a point see Coordinates of a Point

Things you can do in Coordinate Geometry

If you know the coordinates of a group of points you can:

• Determine the distance between them
• Find the midpoint, slope and equation of a line segment
• Determine if lines are parallel or perpendicular
• Find the area and perimeter of a polygon defined by the points
• Transform a shape by moving, rotating and reflecting it.
• Define the equations of curves, circles and ellipses.

Information on all these and more can be found in the pages listed below.

History

The method of describing the location of points in this way was proposed by the French mathematician René Descartes (1596 - 1650). (Pronounced "day CART"). He proposed further that curves and lines could be described by equations using this technique, thus being the first to link algebra and geometry. In honor of his work, the coordinates of a point are often referred to as its Cartesian coordinates, and the coordinate plane as the Cartesian Coordinate Plane.

Triangle

A triangle.

A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ABC.

In Euclidean geometry any three non-collinear points determine a unique triangle and a unique plane (i.e. a two-dimensional Euclidean space).

Types of triangles

By relative lengths of sides

Triangles can be classified according to the relative lengths of their sides:

• In an equilateral triangle, all sides are the same length. An equilateral triangle is also a regular polygon with all angles equal to 60°.^[1]
• In an isosceles triangle, two sides are equal in length. (Traditionally, only two sides equal, but sometimes at least two.)^[2] An isosceles triangle also has two equal angles: the angles opposite the two equal sides.
• In a scalene triangle, all sides and internal angles are different from one another.^[3]

Equilateral	Isosceles	Scalene

By internal angles

Triangles can also be classified according to their internal angles, measured here in degrees.

• A right triangle (or right-angled triangle, formerly called a rectangled triangle) has one of its internal angles equal to 90° (a right angle). The side opposite to the right angle is the hypotenuse; it is the longest side in the right triangle. The other two sides are the legs or catheti^{[citation needed]} (singular: cathetus) of the triangle. Right triangles obey the Pythagorean theorem: the sum of the squares of the two legs is equal to the square of the hypotenuse: a² + b² = c², where a and b are the lengths of the legs and c is the length of the hypotenuse. Special right triangles are right triangles with additional properties that make calculations involving them easier.

• Triangles that do not have a 90° internal angle are called oblique triangles.

• A triangle that has all the internal angles smaller than 90° is an acute triangle or acute-angled triangle.

• A triangle that has one angle larger than 90° is an obtuse triangle or obtuse-angled triangle.

• An equilateral triangle is an acute triangle with all three internal angles equal to 60°.

Right	Obtuse	Acute
	Oblique

[edit] Basic facts

Triangles are assumed to be two-dimensional plane figures, unless the context provides otherwise (see Non-planar triangles, below). In rigorous treatments, a triangle is therefore called a 2-simplex (see also Polytope). Elementary facts about triangles were presented by Euclid in books 1–4 of his Elements, around 300 BCE.

A triangle, showing exterior angle d

The internal angles of a triangle in Euclidean space always add up to 180 degrees. This allows determination of the third angle of any triangle as soon as two angles are known. An external angle, or exterior angle, of a triangle is an angle that is adjacent and supplementary to an internal angle. Any external angle of any triangle is equal to the sum of the two internal angles that it is not adjacent to; this is the exterior angle theorem. The three external angles (one for each vertex) of any triangle add up to 360 degrees.^[4]

The sum of the lengths of any two sides of a triangle always exceeds the length of the third side, a principle known as the triangle inequality.^[5]

Two triangles are said to be similar if and only if each internal angle of one triangle is equal to an internal angle of the other.^[6] In this case, all sides of one triangle are in equal proportion to sides of the other triangle.

A few basic postulates and theorems about similar triangles:

• If two corresponding internal angles of two triangles are equal, the triangles are similar.
• If two corresponding sides of two triangles are in proportion, and their included angles are equal, then the triangles are similar. (The included angle for any two sides of a polygon is the internal angle between those two sides.)
• If three corresponding sides of two triangles are in proportion, then the triangles are similar.^[7]

Two triangles that are congruent have exactly the same size and shape:^[8] all pairs of corresponding internal angles are equal in size, and all pairs of corresponding sides are equal in length. (This is a total of six equalities, but three are often sufficient to prove congruence.)

Some sufficient conditions for a pair of triangles to be congruent (from basic postulates and theorems of Euclid):

• SAS Postulate: Two sides and the included angle in a triangle are equal to two sides and the included angle in the other triangle.
• ASA Postulate: Two internal angles and the included side in a triangle are equal to those in the other triangle. (The included side for a pair of angles is the side between them.)
• SSS Postulate: Each side of a triangle is equal in length to a side of the other triangle.
• AAS Theorem: Two angles and a corresponding non-included side in a triangle are equal to those in the other triangle.
• Hypotenuse-Leg (HL) Theorem: The hypotenuse and a leg in a right triangle are equal to those in the other right triangle.
• Hypotenuse-Angle Theorem: The hypotenuse and an acute angle in one right triangle are equal to those in the other right triangle.

An important case:

• Side-Side-Angle (or Angle-Side-Side) condition: If two sides and a corresponding non-included angle of a triangle are equal to those in another, then this is not sufficient to prove congruence; but if the non-included angle is obtuse or a right angle, or the side opposite it is the longest side, or the triangles have corresponding right angles, then the triangles are congruent. The Side-Side-Angle condition does not by itself guarantee that the triangles are congruent because one triangle could be obtuse-angled and the other acute-angled.

Using right triangles and the concept of similarity, the trigonometric functions sine and cosine can be defined. These are functions of an angle which are investigated in trigonometry.

The Pythagorean theorem

A central theorem is the Pythagorean theorem, which states in any right triangle, the square of the length of the hypotenuse equals the sum of the squares of the lengths of the two other sides. If the hypotenuse has length c, and the legs have lengths a and b, then the theorem states that

The converse is true: if the lengths of the sides of a triangle satisfy the above equation, then the triangle has a right angle opposite side c.

Some other facts about right triangles:

• The acute angles of a right triangle are complementary.

• If the legs of a right triangle are equal, then the angles opposite the legs are equal, acute, and complementary; each is therefore 45 degrees. By the Pythagorean theorem, the length of the hypotenuse is the length of a leg times √2.
• In a right triangle with acute angles measuring 30 and 60 degrees, the hypotenuse is twice the length of the shorter side, and twice the length divided by √3 for the longer side.

For all triangles, angles and sides are related by the law of cosines and law of sines (also called the cosine rule and sine rule).

Points, lines and circles associated with a triangle

There are hundreds of different constructions that find a special point associated with (and often inside) a triangle, satisfying some unique property: see the references section for a catalogue of them. Often they are constructed by finding three lines associated in a symmetrical way with the three sides (or vertices) and then proving that the three lines meet in a single point: an important tool for proving the existence of these is Ceva's theorem, which gives a criterion for determining when three such lines are concurrent. Similarly, lines associated with a triangle are often constructed by proving that three symmetrically constructed points are collinear: here Menelaus' theorem gives a useful general criterion. In this section just a few of the most commonly-encountered constructions are explained.

The circumcenter is the center of a circle passing through the three vertices of the triangle.

A perpendicular bisector of a triangle is a straight line passing through the midpoint of a side and being perpendicular to it, i.e. forming a right angle with it. The three perpendicular bisectors meet in a single point, the triangle's circumcenter; this point is the center of the circumcircle, the circle passing through all three vertices. The diameter of this circle can be found from the law of sines stated above.

Thales' theorem implies that if the circumcenter is located on one side of the triangle, then the opposite angle is a right one. More is true: if the circumcenter is located inside the triangle, then the triangle is acute; if the circumcenter is located outside the triangle, then the triangle is obtuse.

The intersection of the altitudes is the orthocenter.

An altitude of a triangle is a straight line through a vertex and perpendicular to (i.e. forming a right angle with) the opposite side. This opposite side is called the base of the altitude, and the point where the altitude intersects the base (or its extension) is called the foot of the altitude. The length of the altitude is the distance between the base and the vertex. The three altitudes intersect in a single point, called the orthocenter of the triangle. The orthocenter lies inside the triangle if and only if the triangle is acute. The three vertices together with the orthocenter are said to form an orthocentric system.

The intersection of the angle bisectors finds the center of the incircle.

An angle bisector of a triangle is a straight line through a vertex which cuts the corresponding angle in half. The three angle bisectors intersect in a single point, the incenter, the center of the triangle's incircle. The incircle is the circle which lies inside the triangle and touches all three sides. There are three other important circles, the excircles; they lie outside the triangle and touch one side as well as the extensions of the other two. The centers of the in- and excircles form an orthocentric system.

The intersection of the medians is the centroid.

A median of a triangle is a straight line through a vertex and the midpoint of the opposite side, and divides the triangle into two equal areas. The three medians intersect in a single point, the triangle's centroid. The centroid of a stiff triangular object (cut out of a thin sheet of uniform density) is also its center of gravity: the object can be balanced on its centroid. The centroid cuts every median in the ratio 2:1, i.e. the distance between a vertex and the centroid is twice the distance between the centroid and the midpoint of the opposite side.

Nine-point circle demonstrates a symmetry where six points lie on the edge of the triangle.

The midpoints of the three sides and the feet of the three altitudes all lie on a single circle, the triangle's nine-point circle. The remaining three points for which it is named are the midpoints of the portion of altitude between the vertices and the orthocenter. The radius of the nine-point circle is half that of the circumcircle. It touches the incircle (at the Feuerbach point) and the three excircles.

Euler's line is a straight line through the centroid (orange), orthocenter (blue), circumcenter (green) and center of the nine-point circle (red).

The centroid (yellow), orthocenter (blue), circumcenter (green) and barycenter of the nine-point circle (red point) all lie on a single line, known as Euler's line (red line). The center of the nine-point circle lies at the midpoint between the orthocenter and the circumcenter, and the distance between the centroid and the circumcenter is half that between the centroid and the orthocenter.

The center of the incircle is not in general located on Euler's line.

If one reflects a median at the angle bisector that passes through the same vertex, one obtains a symmedian. The three symmedians intersect in a single point, the symmedian point of the triangle.

Computing the area of a triangle

The area of a triangle can be demonstrated as half of the area of a paralellogram which has the same base length and height.

Calculating the area of a triangle is an elementary problem encountered often in many different situations. The best known and simplest formula is:

where A is area, b is the length of the base of the triangle, and h is the height or altitude of the triangle. The term 'base' denotes any side, and 'height' denotes the length of a perpendicular from the point opposite the side onto the side itself.

Although simple, this formula is only useful if the height can be readily found. For example, the surveyor of a triangular field measures the length of each side, and can find the area from his results without having to construct a 'height'. Various methods may be used in practice, depending on what is known about the triangle. The following is a selection of frequently used formulae for the area of a triangle.^[9]

Using vectors

The area of a parallelogram can be calculated using vectors. Let vectors AB and AC point respectively from A to B and from A to C. The area of parallelogram ABDC is then , which is the magnitude of the cross product of vectors AB and AC. is equal to , where h represents the altitude h as a vector.

The area of triangle ABC is half of this, or .

The area of triangle ABC can also be expressed in terms of dot products as follows:

Applying trigonometry to find the altitude h.

Using trigonometry

The height of a triangle can be found through an application of trigonometry. Using the labelling as in the image on the left, the altitude is h = a sin γ. Substituting this in the formula S = ½bh derived above, the area of the triangle can be expressed as:

(where α is the interior angle at A, β is the interior angle at B, and γ is the interior angle at C).

Furthermore, since sin α = sin (π - α) = sin (β + γ), and similarly for the other two angles:

Using coordinates

If vertex A is located at the origin (0, 0) of a Cartesian coordinate system and the coordinates of the other two vertices are given by B = (x_B, y_B) and C = (x_C, y_C), then the area S can be computed as ½ times the absolute value of the determinant

For three general vertices, the equation is:

In three dimensions, the area of a general triangle {A = (x_A, y_A, z_A), B = (x_B, y_B, z_B) and C = (x_C, y_C, z_C)} is the Pythagorean sum of the areas of the respective projections on the three principal planes (i.e. x = 0, y = 0 and z = 0):

Using Heron's formula

The shape of the triangle is determined by the lengths of the sides alone. Therefore the area S also can be derived from the lengths of the sides. By Heron's formula:

where s = ½ (a + b + c) is the semiperimeter, or half of the triangle's perimeter.

Three equivalent ways of writing Heron's formula are

Computing the sides and angles

In general, there are various accepted methods of calculating the length of a side or the size of an angle. Whilst certain methods may be suited to calculating values of a right-angled triangle, others may be required in more complex situations.

Trigonometric ratios in right triangles

Main article: Trigonometric functions

A right triangle always includes a 90° (π/2 radians) angle, here labeled C. Angles A and B may vary. Trigonometric functions specify the relationships among side lengths and interior angles of a right triangle.

In right triangles, the trigonometric ratios of sine, cosine and tangent can be used to find unknown angles and the lengths of unknown sides. The sides of the triangle are known as follows:

• The hypotenuse is the side opposite the right angle, or defined as the longest side of a right-angled triangle, in this case h.
• The opposite side is the side opposite to the angle we are interested in, in this case a.
• The adjacent side is the side that is in contact with the angle we are interested in and the right angle, hence its name. In this case the adjacent side is b.

Sine, cosine and tangent

The sine of an angle is the ratio of the length of the opposite side to the length of the hypotenuse. In our case

Note that this ratio does not depend on the particular right triangle chosen, as long as it contains the angle A, since all those triangles are similar.

The cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse. In our case

The tangent of an angle is the ratio of the length of the opposite side to the length of the adjacent side. In our case

The acronym "SOHCAHTOA" is a useful mnemonic for these ratios.

Inverse functions

The inverse trigonometric functions can be used to calculate the internal angles for a right angled triangle with the length of any two sides.

Arcsin can be used to calculate an angle from the length of the opposite side and the length of the hypotenuse.

Arccos can be used to calculate an angle from the length of the adjacent side and the length of the hypontenuse.

Arctan can be used to calculate an angle from the length of the opposite side and the length of the adjacent side.

The sine and cosine rules

Main articles: Law of sines and Law of cosines

A triangle with sides of length a, b and c and angles of α, β and γ respectively.

The law of sines, or sine rule^[10], states that the ratio of the length of side a to the sine of its corresponding angle α is equal to the ratio of the length of side b to the sine of its corresponding angle β.

The law of cosines, or cosine rule, connects the length of an unknown side of a triangle to the length of the other sides and the angle opposite to the unknown side. As per the law:

For a triangle with length of sides a, b, c and angles of α, β, γ respectively, given two known lengths of a triangle a and b, and the angle between the two known sides γ (or the angle opposite to the unknown side c), to calculate the third side c, the following formula can be used:

Non-planar triangles

A non-planar triangle is a triangle which is not contained in a (flat) plane. Examples of non-planar triangles in non-Euclidean geometries are spherical triangles in spherical geometry and hyperbolic triangles in hyperbolic geometry.

While the internal angles in planar triangles always add up to 180°, a hyperbolic triangle has angles that add up to less than 180°, and a spherical triangle has angles that add up to more than 180°. A hyperbolic triangle can be obtained by drawing on a negatively-curved surface, such as a saddle surface, and a spherical triangle can be obtained by drawing on a positively-curved surface such as a sphere. Thus, if one draws a giant triangle on the surface of the Earth, one will find that the sum of its angles is greater than 180°. It is possible to draw a triangle on a sphere such that each of its internal angles is equal to 90°, adding up to a total of 270°.