Arithmetic progression
In mathematics, an arithmetic progression (A.P.) or arithmetic sequence is a sequence of numbers such that the difference of any two successive members of the sequence is a constant. For instance, the sequence 3, 5, 7, 9, 11, 13... is an arithmetic progression with common difference 2.
If the initial term of an arithmetic progression is a1 and the common difference of successive members is d, then the nth term of the sequence is given by:
and in general
A finite portion of an arithmetic progression is called a finite arithmetic progression and sometimes just called an arithmetic progression.
| |
Sum (the arithmetic series)
The sum of the members of a finite arithmetic progression is called an arithmetic series.
Express the arithmetic series in two different ways:
Add both sides of the two equations. All terms involving d cancel, and so we're left with:
Rearranging and remembering that an = a1 + (n − 1)d, we get:
Product
The product of the members of a finite arithmetic progression with an initial element a1, common difference d, and n elements in total, is determined in a closed expression by
where  denotes the rising factorial and Γ denotes the Gamma function. (Note however that the formula is not valid when a1 / d is a negative integer or zero).
denotes the rising factorial and Γ denotes the Gamma function. (Note however that the formula is not valid when a1 / d is a negative integer or zero).
This is a generalization from the fact that the product of the progression  is given by the factorial n! and that the product
is given by the factorial n! and that the product
for positive integers m and n is given by

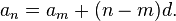



![S_n=\frac{n( a_1 + a_n)}{2}=\frac{n[ 2a_1 + (n-1)d]}{2}.](http://upload.wikimedia.org/math/e/7/2/e721c55a929b0ed536b09091b850be34.png)
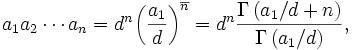


No comments:
Post a Comment